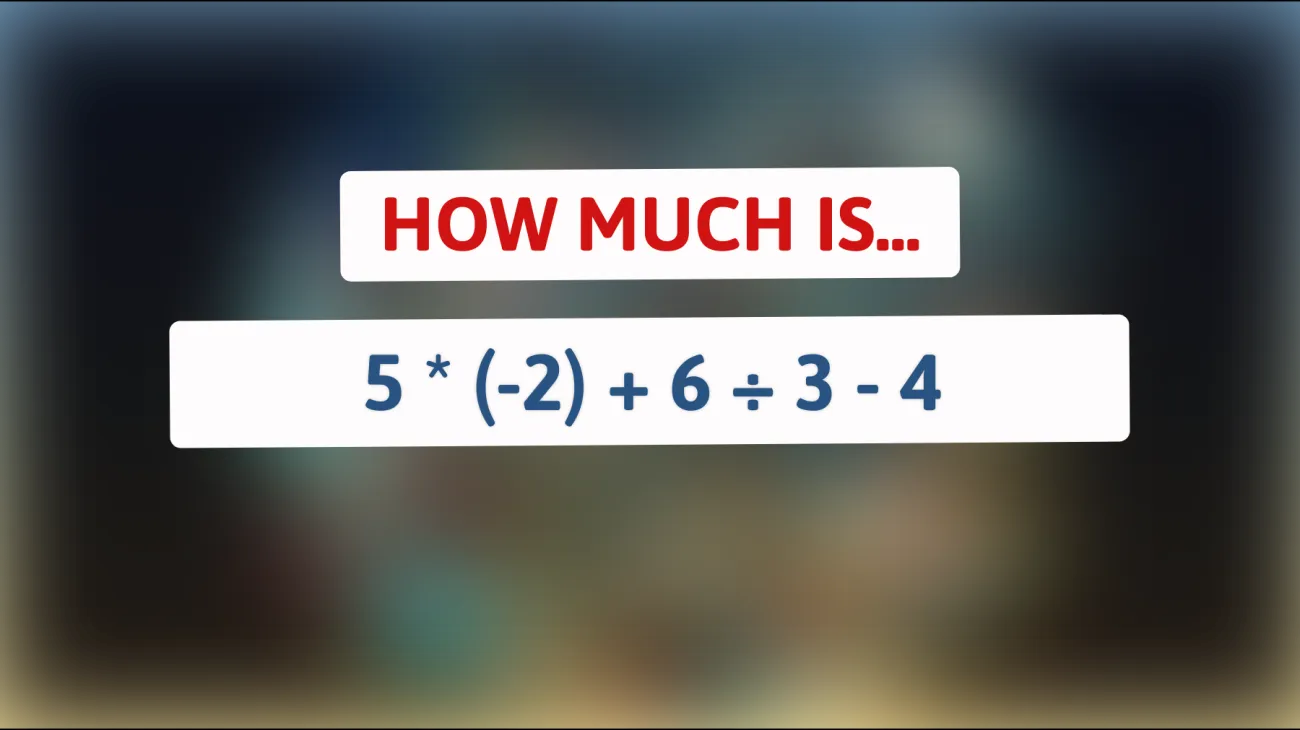Are you prepared to embark on a captivating journey into the world of mathematical puzzles that challenge the very limits of your logical acumen? Dive into the enigma of unraveling how a seemingly simple arithmetic problem reveals profound insights into negative numbers and their intrinsic properties.
Mathematics, often described as the language of the universe, presents riddles that range from the straightforward to the mind-bendingly complex. Among these enigmas, basic arithmetic can often seem deceptively simple; yet, it is within these elementary confines that profound mathematical truths often reside. One such puzzle, presented by the operation: **How much is 5 * (-2) + 6 ÷ 3 – 4?**, beckons you to explore its solution deeply.
To the untrained eye, this arithmetic problem may appear deceptively mundane, a mere exercise in following the basic order of operations. But, herein lies its allure — when approached with a keen intellect and an understanding of fundamental mathematical principles, it unveils layers of complexity. As you embark on deciphering the product of numbers, divisions, and sequential additions followed by subtractions, each step in solving this enigma beholds a revelation of its own.
Solving a Math Problem: Delving into Negative Number Dynamics
At first glance, solving the puzzle appears to be a straightforward application of mathematical conventions. You begin with multiplication: **5 * (-2)**, a foundational task that yields **-10**. This step serves as an introduction to the puzzling nature of negative numbers and their inherent impact when multiplied with positive integers—a figurative dance where opposites intertwine.
Onwards to the division: a simple operation of **6 ÷ 3** produces the quotient **2**, reinforcing the role that division plays in balancing our arithmetic scales. As we integrate this newly found quotient into our evolving equation: **-10 + 2**, we encounter the subtle complexities of addition and subtraction—that which arises from contrasting signs. This initial operation leads us to a provisional result of **-8**, serving as a prelude to the problem’s grand culmination.
Unraveling the Mathematical Riddle: Understanding -9
The final act of this arithmetic performance requires the subtraction of **4** from **-8**, guiding our cerebral journey to the nuanced, yet definitive, solution of **-9**. This number, **-9**, is more than a concluding value; it holds significant mathematical curiosity. As the negation of the smallest positive odd number, it also parallels the negation of the ninth Fibonacci number. Engaging with this simple problem, therefore, not only reinforces foundational concepts of basic operations and negative numbers but invites a broader contemplation on the inherent beauty of numerical patterns that underpin much of mathematics.
To unravel how **5 * (-2) + 6 ÷ 3 – 4** leads to **-9** is to partake in a symphony of numeric harmonies. Each step in the solution serves as a reminder that even the most modest of mathematical problems can contain multitudes, waiting to be discovered by those willing to delve deeper. Such riddles are not merely exercises in computation, but intellectual endeavors inviting curiosity and encouraging exploration, unlocking the artistic tapestry that mathematics so elegantly weaves.